![[Next]](../images/b_next.gif)
![[Prev]](../images/b_prev.gif)
![[Contents]](../images/b_contents.gif)
![[Top]](../images/b_top.gif)
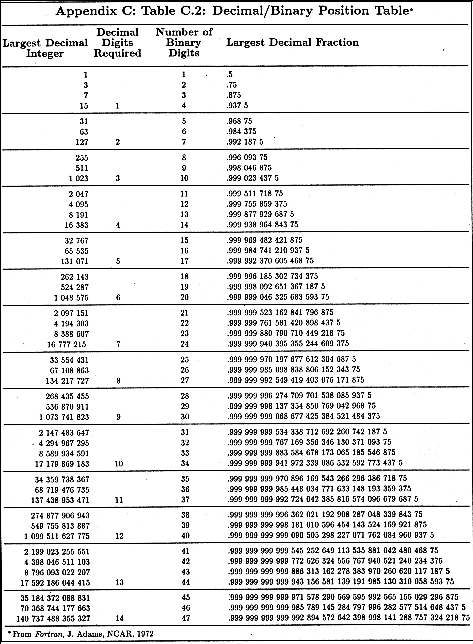
Two similar methods are often used to create a packed binary value. The first method uses three elements: a sign bit (e.g., 0 for a positive number and 1 for a negative number), a reference value (sometimes called an `offset') and a scaling constant. The second method uses only a reference value and a scaling constant. The basic idea is to create a number which is a non-negative scaled difference from a reference value. To design an optimized packed binary format requires knowledge of the precision and range of possible data values. Thus, most packed binary data sets are custom designed. As a simple example, consider values from numerical computations or from measurements which have the range -99.0 to 100.0 and where the desired precision is tenths. Then, the reference value might be 100 and the scale factor could be 10. Table C.1 illustrates the steps to pack (left hand column) and unpack (right hand column) a number. Appendix C.2 provides a table which indicates the number of binary digits required to represent a decimal integer.
| Packing | Unpacking | ||
|---|---|---|---|
| value to be packed | 13.4 | value to be unpacked | 866 |
| add reference value | -13.4 + 100. | unscale | 866/10 |
| store as real | 86.6 | store as real | 86.6 |
| scale value | 86.6 * 10. | subtract reference | 100. - 86.6 |
| resulting positive integer | 866 | value | 13.4 |
| sign bit | 1 | sign bit | -13.4 |

![[Next]](../images/b_next.gif)
![[Prev]](../images/b_prev.gif)
![[Contents]](../images/b_contents.gif)
![[Top]](../images/b_top.gif)